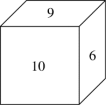
6.(单选题)如图，一个正方体的表面上分别写着连续的6个整数，且每两个相对面上的两个数的和都相等，则这6个整数的和为：

　　A.53

　　B.52

　　C.51

　　D.50

　　解析

　　解法一：

　　第一步，本题考查基础计算问题。

　　第二步，已知6、9、10三个数，则6个连续整数可能是(5，6，7，8，9，10)或者(6，7，8，9，10，11)两种情况。前者6和9在相对面上，与图形不符;或前者加和为45，选项没有此答案直接排除。因此6个整数的和为6+7+8+9+10+11=51。

　　因此，选择C选项。

　　解法二：

　　第一步，本题考查基础计算问题，用数字特性法解题。

　　第二步，3组相对面，每组相对面的和相等，设其为n，则总和为3n，即为3的倍数;或者6个连续的整数之和为3的倍数。只有C符合。

　　因此，选择C选项。

　　7.(单选题)某种农作物原来亩产为 600 千克，改进种植技术后，亩产增加100千克，且由于品质改善，每千克的售价提高 1元，每亩产值比之前增加1100元。则原来每亩产值是多少元?

　　A.1800

　　B.2100

　　C.2400

　　D.2700

　　解析

　　第一步，本题考查经济利润问题中的基础公式类。

　　第二步，改进种植技术后，亩产为600+100=700千克。设原来每千克售价为x元，列方程：700(x+1)-600x=1100，解得x=4，则原来每亩产值是600×4=2400元。

　　因此，选择C选项。

　　8.(单选题)甲、乙、丙、丁等4人去完成四项任务，并要求每人只完成一项任务，每一项任务只能由一人完成，每人完成各项任务的所用时间(单位：小时)如下表：

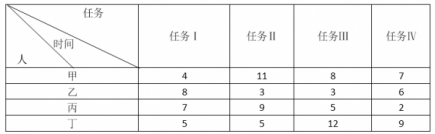
　　则最优分配方案是：

　　A.甲-任务Ⅰ，乙-任务Ⅱ，丙-任务Ⅳ，丁-任务Ⅲ

　　B.甲-任务Ⅰ，乙-任务Ⅲ，丙-任务Ⅱ，丁-任务Ⅳ

　　C.甲-任务Ⅳ，乙-任务Ⅱ，丙-任务Ⅲ，丁-任务Ⅰ

　　D.甲-任务Ⅰ，乙-任务Ⅲ，丙-任务Ⅳ，丁-任务Ⅱ

　　解析

　　解法一：

　　第一步，本题考查统筹推断问题。

　　第二步，要想最优方案，则所有人尽量按效率高的来分工，观察题目表格与选项差别，对于甲最适合的任务是Ⅰ，排除C;对于丙，最合适的是任务Ⅳ，排除B;任务Ⅱ与任务Ⅲ，对于乙和丁，其中乙干任务Ⅲ、丁干任务Ⅱ更优化。

　　因此，选择D选项。

　　解法二：

　　第一步，本题考查统筹推断问题。

　　第二步，要想最优方案，则所有人尽量按效率高的来分工，完成的时间越短即效率越高。如表所示：

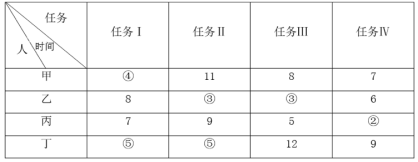
　　甲适合做任务Ⅰ，乙适合做任务Ⅱ和任务Ⅲ，丙适合做任务Ⅳ，丁适合做任务Ⅰ和任务Ⅱ。统筹考虑，甲做任务Ⅰ，乙做任务Ⅲ，丙做任务Ⅳ，丁做任务Ⅱ。

　　因此，选择D选项。

　　9.(单选题)某宾馆有6个空房间，3间在一楼，3间在二楼。现有4名客人要入住，每人都住单间，都优先选择一楼房间。问宾馆共有多少种安排?

　　A.24

　　B.36

　　C.48

　　D.72

　　解析

　　第一步，本题考查排列组合题，属于基础排列组合。

　　10.(单选题)一副扑克牌有52张，最上面一张是红桃A。如果每次把最上面的10张移到最下面而不改变它们的顺序及朝向，那么，至少经过多少次移动，红桃A会出现在最上面?

　　A.27

　　B.26

　　C.25

　　D.24

　　解析

　　第一步，本题考查约数倍数问题。

　　第二步，根据每次把最上面的10张移到最下面，可知移动的扑克牌张数是10的倍数;由红桃A从最上面再回到最上面，可知移动的扑克牌张数是52的倍数，即至少需要移动260(10和52的最小公倍数)张扑克牌，红桃A才能再次出现在最上面。

　　第三步，故至少经过260÷10=26(次)移动。

　　因此，选择B选项。