第1周（周三）数量关系解析
第1周周三上午数量：解题思想
（本部分共20题，参考时限30分钟）
1.C【解析】余数问题，选项除以7余1，A、D不满足，排除。余下B、C两个选项，任意代入其中一个即可得出最终选项。代入B，不满足第二个条件，排除。因此，本题选择C选项。
2.A【解析】甲队人数最多，因此，甲队＞6人，乙队+丙队＜9人，丁队＞4人，排除C、D。余下A、B两个选项，任意代入其中一个即可得出最终选项。代入A，甲队9人，乙队+丙队=6人，可满足题意（若代入B，甲队10人，与“每支分队人数均为个位数”相悖，排除）。因此，本题选择A选项。
3.D【解析】代入A选项，X、Y只能等于0和1，不符合题意，排除A选项；B选项，X、Y只能等于1和2，Z=2不等于1+2+3，排除B选项；C选项，若X、Y等于1和4，Z=4不等于1+4+3，若X、Y等于2和3，Z=6不等于2+3+3，排除C选项；D选项，若X、Y等于2和5，Z=10=2+5+3，满足题意。因此，本题选择D选项。
4.A【解析】赋值乙班30人，则甲班20人，丙班15人。20/（20+30+15）=4/13。因此，本题选择A选项。
5.D【解析】设甲、乙、丙社区人口分别为12人、8人、7人，则甲社区常住人口与外来人口分别为3人与9人，乙社区常住人口与外来人口分别为3人与5人，丙社区常住人口与外来人口分别为x人与（7-x）人，则（3+3+x）：（9+5+7-x）=1：2，解得x=3，故丙社区常住人口与外来人口比为3：4。因此，本题选择D选项。
6.C【解析】直接代入即可。
7.A【解析】根据题意，设应用x张铁皮制作盒身，那么2×16x=43（150-x），x=86。因此，本题选择A选项。
8.A【解析】方法一：设第一次有n包，第二次有m包，则5n+8=6m，3n=2m+8，解得m=n=8，因此共有图书8m+8=72本书。因此，本题选择A选项。
方法二：若从第一次包裹中每包各抽取一本工具书，最后剩下8本，说明第一次有8包书本，因此书本总数=8×8+8=72。因此，本题选择A选项。
9.C【解析】方法一：设原来男女分别为2x、5x，可得（2x+4）/5x=3/5，解得x=4，故原金融班里有男生2x=8人。因此，本题选择C选项。
方法二：金融班转入4个男学生，男女学生的比例为3：5，则原来的男生人数加上4的和应该是3的倍数，选项中只有C满足。因此，本题选择C选项。
方法三：原来的男女比例为2：5，后面变为3：5，女生人数不变，男生人数增加了1份，则1份相当于4人，则原来的2份相当于8人。因此，本题选择C选项。
10.C【解析】设甲班x人，乙班y人，列方程组，得：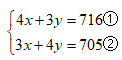
。①式＋②式得，7（x+y）=1421，解得x+y=203。因此，本题选择C选项。
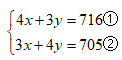。①式＋②式得，7（x+y）=1421，解得x+y=203。因此，本题选择C选项。
11.C【解析】3×（86+92+100+106）=6×（四次分数的总和），所以四次分数总和192，即四次考试的平均分为48。因此，本题选择C选项。
12.B【解析】本题属于多位数问题，考虑代入排除法，题目求的是“最多”，从最大的数字开始代入。D项，960不是35的倍数，排除；C项，855不是35的倍数，排除；B项，630÷35＝18，630——360＝270，满足题意。因此，本题答案选择B选项。
13.A【解析】设较大的数为x，较小的数为y，则x+y=28。代入A选项，若x-y=16，解得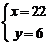
，而144÷6=24，大于22，则满足题目条件。同理验证B、C、D都不满足题意。因此，本题选择A选项。
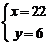，而144÷6=24，大于22，则满足题目条件。同理验证B、C、D都不满足题意。因此，本题选择A选项。
14.C【解析】第一只猴子吃掉1个后，剩下的平均分成5份，可知总数减1后能被5整除，排除A、B两项。题目要求“最少”，代入最小的D项，2101——1＝2100，2100÷5＝420，剩余2100——420＝1680；1680——1＝1679，不能被5整除，排除D项。因此，本题选择C选项。
15. 15.C【解析】方法一：设甲班有x人，乙班有y人，根据题意可得，即4x＋5y＝472。4x是偶数，472是偶数，则5y一定是偶数，即y是偶数，排除B、D两项。代入A项，y＝46时，x＝60.5，不合题意，排除A项。代入C项，y＝48时，x＝58，两班分别买票需要58×8＋48×10＝944元，联合买票需要（58＋48）×5＝530元，符合。因此，本题选择C选项。
方法二：设甲班有x人，乙班有y人，两班一起购票价格为530元，不是8的倍数，则人数之和一定大于100，可得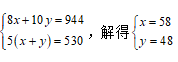
。因此，本题选择C选项。
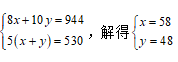。因此，本题选择C选项。
16.B【解析】方法一：根据题意可知，总人数减去8之后一定是12的倍数，排除A、C、D三项。因此，本题选择B选项。
方法二：设男员工x人、女员工y人，可得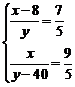
，解得
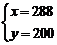，故员工总数为288＋200＝488人。因此，本题选择B选项。
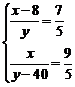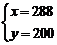，解得，故员工总数为288＋200＝488人。因此，本题选择B选项。
方法三：最开始减去8名男员工，男女之比为7：5；若保持女员工人数不变，使男女之比为9：5，需要增加男员工为
人。设最开始男员工人数为7份，女员工人数是不变的为5份，则男员工人数增加80人变为9份，则每份为40人，则女员工人数为5×40＝200人，男员工人数为7×40＋8＝288人，共有员工200＋288＝488人。因此，本题选择B选项。
人。设最开始男员工人数为7份，女员工人数是不变的为5份，则男员工人数增加80人变为9份，则每份为40人，则女员工人数为5×40＝200人，男员工人数为7×40＋8＝288人，共有员工200＋288＝488人。因此，本题选择B选项。
17.C【解析】见习人员是驾驶员和船员的1/4，则驾驶员、船员、见习驾驶员、见习船员的总人数为5的倍数；船员（含见习船员）总人数是驾驶员（含见习驾驶员）总数的7倍，则驾驶员、船员、见习驾驶员、见习船员的总人数为8的倍数，则驾驶员、船员、见习驾驶员、见习船员的总人数必须为40，则陆战队员为60——40＝20人。因此，本题选择C选项。
18.B【解析】第一步，标记量化关系“不超过”。“最高”。第二步，投票有效率“最高”，则有效投票张数最高，根据“不超过”，则有效票数“最高”情况为：一部分票恰好投2幅作品，且剩下票数都投5幅作品。设总票数为100张，投2幅作品人数为x，列式为2x+5×（100-x）=69+63+44+58+56=290。第三步，解得x=70，则投票有效率为70÷100=70%。因此，本题选择B选项。
19.D【解析】设小明、小强和小军购买的课外书分别为x、y、z本，则可得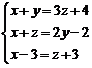
解得
。因此，本题选择D选项。
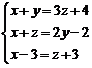解得。因此，本题选择D选项。
20.C【解析】方法一：小王、小李、小张、小周分别捐了a、b、c、d个，可得a＞b＞c＞d，且a＝b＋c，b＝c＋d，可得a＋b＋c＋d＝4c＋3d＝25，可解得d＝3、c＝4，b＝c＋d＝7，a＝b＋c＝11。因此，本题选择C选项。
方法二：本题可采用代入排除法。A项，假设小王捐了9个书包，则小李捐了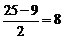
个，小张捐了9——8＝1个，小周捐了8——1＝7个，不符合题意，排除。B项，假设小王捐了10个书包，则小李捐了
个，不合题意，排除，且同理可排除D项。C项，假设小王捐了11个书包，则小李捐了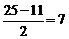
个，小张捐了11——7＝4个，小周捐了7——4＝3个，符合题意。因此，本题选择C选项。
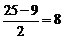个，小张捐了9——8＝1个，小周捐了8——1＝7个，不符合题意，排除。B项，假设小王捐了10个书包，则小李捐了个，不合题意，排除，且同理可排除D项。C项，假设小王捐了11个书包，则小李捐了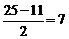个，小张捐了11——7＝4个，小周捐了7——4＝3个，符合题意。因此，本题选择C选项。
第1周周三下午数量：初等数学、等差数列、工程问题（本部分共20题，参考时限30分钟）
1.D【解析】逐个分析每个数字（1-10）的约数个数，10的约数有1、2、5、10，故10共被翻转四次，仍然背面向上；9的约数有1、3、9，共被翻转三次，正面向上。1的约数只有1，故向上。故正面向上的最大编号和最小编号分别为9、1，差值为8。因此，本题答案选择D选项。
2.D【解析】每报三个数字，才能有一个人表演，29个人表演完，需要报数29×3＝87次。因此，本题选择D选项。
3.C【解析】每次装水量都是上一次的两倍，第一次使水升高5厘米，则第2、3、4次水位分别升高10、20、40厘米，水深为5＋10＋20＋40＝75厘米，离鱼缸顶部还有15厘米，则鱼缸的高度为75＋15=90厘米。因此，本题选择C选项。
4.B【解析】两红两黄组成的长方形面积应为红黄木棍长度的乘积，于是有红黄乘积为20，红蓝乘积为28，黄蓝乘积为35，所以蓝色木棍长度应为28、35的公约数，只有B选项满足。
5.A【解析】羽＝2乒①，足＝3篮②，4乒＝羽＋足＋篮③，其中①③联立容易化简，所求为羽毛球，将①代入③，可得2羽＝羽＋足＋篮，即羽＝足＋篮。因此，本题选A。
6.C【解析】题中没有给出具体数值，考虑赋值。设A前三季度完成100，则B前三季度完成120，则B全年完成120/3＋120＝160，则A全年完成192，可得A第四季度完成92，前三季度平均完成100/3，则第四季度业绩是前三季度平均值的92÷（100/3）＝2.76。因此，本题选C。
7.D【解析】“每隔3天去一次”意思是“每四天去一次”。因此4，5，6最小公倍数60，60天之后三人再次相遇。2016年2月是闰月，有29天，3月31天，加起来正好60天，下一次相遇即为4月10日。因此，选择D选项。
8.B【解析】要使银杏树最多，考虑极限情况，只需要从一侧一端开始就种植银杏树。那么一侧每隔3棵银杏树种1棵梧桐树，即每4棵中的前3棵为银杏树，35÷4＝8……3，则银杏树为3×8＋3＝27棵；另一侧每隔4棵梧桐树种1棵银杏树，即每5棵的第1棵为银杏树，35÷5＝7，则银杏树有7棵；27＋7＝34棵。因此，本题选B。
9.C【解析】由题意，因为三人轮流主持会议，副主编第12次主持会议时，其实是第36次会议，前面经历了35次会议周期，每个周期一个礼拜7天，所以最后主持会议的日期应该是第一次会议1月6日之后的第35×7=245天。所以日期推断为25（一月）+28（二月）+31（三月）+30（四月）+31（五月）+30（六月）+31（七月）+31（八月）+8（九月）=245。因此，选择C选项。
10.A【解析】1-12日的日期数字之和为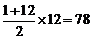
，三人的值班日期数字之和相同，均为78÷3＝26。甲头两天值班，这两天的日期数字之和为1＋2＝3，还缺26——3＝23，只能由11＋12构成，所以甲的值班日期可以确定为1、2、11、12日。乙9日、10日值班，这两天的数字之和为9＋10＝19，还缺26-19＝7，只能由3＋4构成，所以乙的值班日期可以确定为3、4、9、10日，因此丙的值班日期为5、6、7、8日，在自己第一天与最后一天值夜班之间，有0天。因此，本题选择A选项。
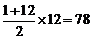，三人的值班日期数字之和相同，均为78÷3＝26。甲头两天值班，这两天的日期数字之和为1＋2＝3，还缺26——3＝23，只能由11＋12构成，所以甲的值班日期可以确定为1、2、11、12日。乙9日、10日值班，这两天的数字之和为9＋10＝19，还缺26-19＝7，只能由3＋4构成，所以乙的值班日期可以确定为3、4、9、10日，因此丙的值班日期为5、6、7、8日，在自己第一天与最后一天值夜班之间，有0天。因此，本题选择A选项。
11.B【解析】设总共有N名选手，小周排名为x，可得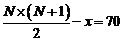
，即
。代入选项可得，当x＝8时，可得N＝12，符合题意。因此，本题选择B选项。
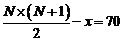，即。代入选项可得，当x＝8时，可得N＝12，符合题意。因此，本题选择B选项。
12.D【解析】上面一级比下面一级多站一个人时，五个台阶上的人数为N、N——1、N——2、N——3、N——4，台阶上站的总人数为5N—10人；上面一级比下面一级少站一个人时，五个台阶上的人数为N、N＋1、N＋2、N＋3、N＋4，台阶上站的总人数为5N+10人，则第二次需要的人数比第一次多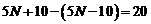
人。第一次多了7个人，则第二次少了20——7＝13人。因此，本题选择D选项。
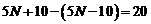人。第一次多了7个人，则第二次少了20——7＝13人。因此，本题选择D选项。
13.B【解析】设王强的效率为x，李雷的效率为y，由题意可得40x=30y+20（x+y），解得x：y=5：2，赋值各自效率为5、2，则总量为40×5=200。王强是工作一天休息一天，则两天内两人的效率和为5+2+2=9，200÷9=22余2，余下的2可以在1天内完成，则共需22×2+1=45天。因此，本题选择B选项。
14.C【解析】根据题意可赋值十级工的效率为4，六级工的效率为2，设八级工的效率为x，依据题意可得：（4+2x）×5×7=（x+2×2）×50，解得x=3，则合作效率为9，总量为400，共需45天。因此，本题选择C选项。
15.C【解析】根据题意，甲+丙=乙，甲+乙=4丙，可以得出甲：乙：丙=3：5：2，赋值他们的效率分别是3、5、2，代入合作时间30得出总量是300，用300除以3，所以是100。因此，本题选择C选项。
16.A【解析】设每人每天的效率为1，则总的工作量为2×100+5×70+5×50=800，10天修完需要800÷（10×1）=80人。因此，本题选择A选项。
17.B【解析】假设每天的工作效率为1，20天完成则总量为20，如果16天完成了，那么每天的实际效率应为20÷16=1.25，所以效率提高了25%。因此，本题选择B选项。
18.C【解析】设乙每小时加工x个零件，则甲每小时加工1.3x。由此可得：8（x+1.3x）=736，解得x=40。因此，本题选择C选项。
19.C【解析】设全长为24x，则甲每天可以铺3x。由此可得12x+200=16x，解得x=50，所以全长24x=1200。因此，本题选择C选项。
20.A【解析】赋值工作总量为60，设甲乙丙的效率分别为x，y，z，则有x+y=6，y+z=5，4（x+z）+12y=60。解得y=4，故全部由乙完成的话需要60÷4=15。因此，答案选择A选项。
