排列的定义:从n个不同元素中,任取m(m≤n,m与n均为自然数,下同)个不同的元素按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列;从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号A(n,m)表示。
计算公式:
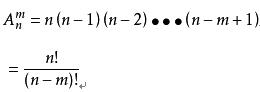
此外规定0! = 1 (n!表示n(n-1)(n-2)...1,也就是6!=6x5x4x3x2x1)
组合的定义:从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。用符号C(n,m) 表示。
计算公式:
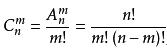
;C(n,m)=C(n,n-m)。(n≥m)
学完基础概念,我们一起通过例题来巩固一下基础知识。
【例1】两对夫妇各带一个小孩乘坐有6个座位的游览车,游览车每排只有1个座位。为安全起见,车的首尾两座一定要坐两位爸爸;两个小孩一定要排在一起。那么,这6人的排座方法有:
A. 12种 B. 24种
C. 36种D. 48种
【答案】B
【解题思路】
第一步,标记量化关系“在一起”。
![]()
第二步,先将两位爸爸安排在首尾两座,则有种方法,再将两个小孩看成一个整体,与两位妈妈一起排列,则有种方法。
![]()
第三步,6人的排座方法共有种。因此,选择B选项。










