国省考公务员行测备考之数量关系的多集合容斥问题

　　公考数量关系中有些类型的题公式多，变化多，想清楚的掌握这些类型的题需要大量的精力，但是有一些类型的题相对来说方法比较固定，较易掌握， 比如工程问题， 容斥问题 。 今天就给大家介绍关于容斥问题的相关内容 。

　　一 、题型特点：题干中出现总人数， 满足A条件的人数，满足B条件的人数，满足C条件的人数，满足AB条件的人数，满足BC的人数，满足AC的人数，满足ABC的人数，总人数等这些量中的部分量，求其中某个未知量。

　　二、 解题方法 : 可直接通过公式或画图求解

　　二 集合容斥公式 ：

　　A+B-A∩B=A∪B=总数-都不满足的情况数

　　三集合标准型公式：

　　A+B+C-A∩B-A∩C-B∩C+A∩B∩C=A∪B∪C=总数-都不满足的情况数

　　三集合非标准型公式：

　　A+B+C-只满足两个条件-满足三个条件×2=A∪B∪C=总数-都不满足的情况数

　　当题干 中所给的数据不足或所求量非以上公式中的量时，考虑赋值法。

　　三、真题感知

　　【例 1 】 240 名学生中报文化课辅导班的与未报文化课辅导班的人数比是 5:3 ， 报艺术 辅导班的与未报艺术辅导班的人数比是 7:5 ，两类辅导班都报的有 86 人，则两类辅导班都没有报的人数是?

　　A.36 人 B.42 人

　　C.48 人 D.54 人

　　【答案】 A

　　【解析】 第一步，本题考 查 二 集合 容斥问题 ，可直接利用公式法求解。

　　第二步，根据题干总人数为 2 40 人， 报 文化课辅导班的与未报文化课辅导班的人数比是 5:3 ， 报艺术 辅导班的与未报艺术辅导班的人数比是 7:5 。可得报文化 课 辅导班的有 (人)， 报 艺术 辅导班的 有 (人)。

　　第三步，设 两类辅导班都没有报的人数 为 x ，直接代入公式 1 50+140-86 = 240- x ，解得 x= 36 。

　　因此，选择 A 选项。

　　上题 是 直接 利用标准公式求解的，接下来我们看一个利用非标准型公式求解的 例题。

　　【例 2 】 某专业 55 名同学都报名参加了大学生社团，有 35 人参加了滑冰社， 28 人参加了书法社， 31 人参加了吉他社，以上三个社团都参加的有 6 人，只参加一个社团的有 ( ) 人。

　　A.22 B.29

　　C.33 D. 5

　　【答案】 A

　　【解析】 第一步，本题考查三 集合容斥问题 。

　　第二步，题干求只参加一个 社团 的 人数，由于没有都不参加的，题干所求即为下图中三个圆中的空白部分 。 图中 ② 表示 只满足 2 种情况的总 人 数 ， ③ 表示 同时满足 3 种情况的 人 数 即 6 人 。

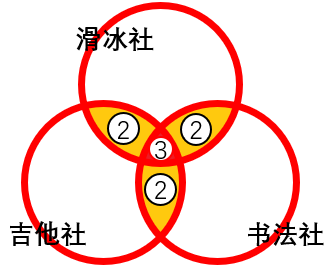
　　第三步，代入非三集合标准型公式， 35+28+31 - ② - 2 × 6= 55-0 ，得 ② = 27 (人)，故所求为 55-27-6 = 22 (人)。

　　因此，选择 A 选项。

　　相信大家通过这两道 题可以 清楚的 了解到，虽然 容斥问题 中给的数据比较多，但是相对 来说做法 比较固定 ， 能用公式的直接套用公式， 不能直接通过公式的结合画图解决 。 因此 大家一定要准确的记忆公式， 这样才能 灵活的运用 到容斥问题 中 。