2018国家公务员考试公告已于2017年10月28日发布,笔试时间为2017年12月10日。湖北华图特将2018国考行测备考:多集合反向构造,不怕发布如下,并将持续更新。湖北人事考试网(http://hb.huatu.com/)将及时更新国家公务员、湖北公务员、湖北事业单位等招考资讯。考生敬请关注【2018国考刷题群: 584211943】,咨询电话:027-87870401
相关推荐:国考公告♦报名入口♦职位表♦报考指南 ♦ 国考日程

多集合反向构造问题是构造问题的延伸,同学们往往在刚接触这类题型的时候会摸不着头脑:感觉题目看起来有些像集合问题,但与集合问题的问法却不同;感觉像最不利构造问题,但在题型匹配上和普通的构造问题的特征却不符。这类多集合反向构造问题看似很复杂,但只要掌握了其特点、原理及方法,其实是可以做到快速解题的。接下来我们一起来学习一下多集合反向构造。
【题目特征】
“…都…至少…”
这类题型中一个很重要的特征就是,问题中会出现“…都…至少…”或类似意思的表达,当出现这种情况时,我们可以考虑是多集合反向构造题。
【方法分析】
我们先结合一道例题看一下:
【例】阅览室有100本杂志,小赵借阅过其中75本,小王借阅过70本,小刘借阅过60本,则三人共同借阅过的杂志最少有( )本。
A.5B.10
C.15D.30
分析题意,要使“三人共同借阅过的杂志最少”,即三人都借阅过的杂志至少的意思,出现了相应的题目特征。我们从正面思考有些困难,可以从反面尝试解题,“最少”的反面是最多,“共同借阅过”的反面是三人都没有借阅过,要使“三人共同借阅过的杂志最少”的反面也就是使三人都没有借阅过的杂志最多。所以这道题实际上我们求的正面=总量-反面,即最少情况下三人共同借阅过的杂志数=(100-最多情况下三人都没有借阅过的杂志数)。
那么问题来了,如何使三人都没有借阅过的杂志数最多?三人没有借阅过的杂志数,可以用题目条件给出的杂志总数100,减去三人分别借阅过的杂志数75、70、60本,得到25、30、40本,要使都没有借阅过的杂志数最多,也就是三人没有借阅过的杂志间没有重复的部分,所以都没有借阅过的杂志数最多为25+30+40=95,那么这道题所求即为100-95=5本。
我们也可以结合集合的概念来理解:
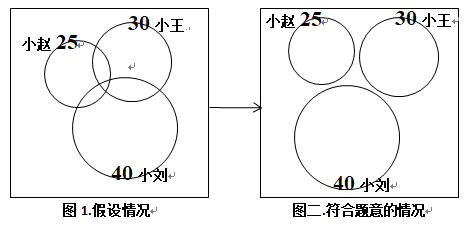
我们把杂志总数用方框表示,把三人没有借阅过的杂志数分别用3个圆圈表示,那么这几个圆圈间就可能存在重合的部分,也可能没有重合,我们不清楚,假设他们三人两两间都有重合(如图一),那么圆内代表没有借阅的杂志数,则在圆外同时在框内的部分代表的就是三人共同借阅过的杂志数,也就是题目所求量。

根据题意,要使所求量尽量小,也就是要使3个圆共同覆盖的面积尽量大,那么什么情况下最大呢?只有三圆没有重合的时候共同覆盖面积才是最大的(如图二)。所以题目所求的三人共同借阅过的杂志最少,即圆外框内的部分=总数100-(25+30+40)=5本【答案】A
【方法总结】
这类题目我们通过“…都…至少…”的特征判定了题目类型后,解题步骤可以分为3步:
反向:正面思考问题困难,我们从反面着手,求出所给条件的反面。
比如问的是“共同借阅过的杂志最少”,反面是“都没有借阅过的杂志数最多”,分别求出没有借阅的数量是25、30、40本。
求和:求出所有反面情况之和。
比如要使都没有借阅过的杂志数最多,即没有借阅的数量间没有重合,故没有借阅过的杂志数最多为25+30+40=95(本)。
作差:用总数减去反面情况之和。
杂志总数-反面,即100-95=5(本)
明白了方法,我们一起用一道题练习一下:
【练习】某班有70%的学生喜欢打羽毛球,75%的学生喜欢打乒乓球,问喜欢打乒乓球的学生中至少有百分之几喜欢打羽毛球?( )A.30%B.45%
C.60%D.70%
【答案】C
【解析】首先判别题型,问题“喜欢打乒乓球的学生中至少有百分之几喜欢打羽毛球?”即求使乒乓球和羽毛球都喜欢打的学生人数至少时,其占打乒乓球学生人数的比例。出现了“…都…至少…”的题目特征,判断为多集合反向构造问题。由于题目给出数据都是百分数,我们可设这个班级有100名学生,则喜欢打羽毛球和乒乓球的分别为70、75人,第一步,反向,求出不喜欢打羽毛球和乒乓球的分别为30、25人;第二步,求和,不喜欢打羽毛球和乒乓球的人数最多=30+25=55;第三步,作差,同时喜欢这两种球类运动的人数至少为100-55=45;最后,根据题目问题,占喜欢打乒乓球的学生的比重为45÷75=60%,即喜欢打乒乓球的学生中至少有60%喜欢打羽毛球。因此,本题选择C选项。
【小结】在了解了多集合反向构造的原理及方法后,同学们是否感到这类题目不再那么可怕了?其实步骤很简单,但一定要记得结合题目具体要求,灵活解题哦!










