2018年国家公务员考试笔试将于2017年12月10日举行,考生提前做好2018年国家公务员考试备考。湖北人事考试网【微信号:huatu027】特将2018国考行测备考:增长量计算之一招鲜,吃遍天!发布如下,供考生参考。欢迎考生加入QQ群【2018国考刷题群:584211943】。咨询电话:027-87870401
课程推荐:2018国家公务员考试课程
重磅推荐:看书刷题听课 尽在公考盒子

增长量是在资料分析里面常出现的一种考法,其本质就是计算现期量和基期量之间的绝对差距。而与之相对应的增长率则是计算现期量和基期量之间的相对差距。也正是因为如此,很多考生总区分不开这两种题型,下面通过一张表格来进行对比:
| 异同点/题型 | 增长量题型 | 增长率 |
| 相同点:设问方式 | 增长(加)/增长(加)了多少…… | |
| 不同点:单位 | 文字单位:人、个、元、吨…… | % |
通过上表不难发现增长量与增长率主要的区别就是单位,那么在了解题型判断之后,我们重点来看这个能一招解决增长量计算的方法是什么?
其实最简单的算法就是:增长量=现期量-基期量。如果题目材料都给出了那么直接相减即可,但是通常大部分的资料给出的往往是现期量和增长率,因此增长量计算可写为: 。如果用字母来表示可简化为:
。如果用字母来表示可简化为: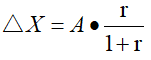 。但是这个算式依然不是最简单的,我们还可以继续化简——若r=1/n,那么
。但是这个算式依然不是最简单的,我们还可以继续化简——若r=1/n,那么 最后化简可得:
最后化简可得: 。
。
 。如果用字母来表示可简化为:
。如果用字母来表示可简化为: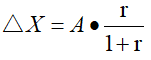 。但是这个算式依然不是最简单的,我们还可以继续化简——若r=1/n,那么
。但是这个算式依然不是最简单的,我们还可以继续化简——若r=1/n,那么 最后化简可得:
最后化简可得: 。
。
对,就是这一招!请牢记!不过在使用前必须先记住下表中常用常考的特殊分数:
| 1/2=50% | 1/3≈33.3% | 2/3≈66.7% | 1/4=25% |
| 1/5=20% | 1/6≈16.7% | 1/7≈14.3% | 1/8=12.5% |
| 1/9≈11.1% | 1/10=10% | 1/11≈9.1% | 1/12≈8.3% |
| 1/13≈7.7% | 1/14≈7.1% | 1/15≈6.7% | ...... |
有了这些工具增长量计算类的题目就能轻松拿下了,等不及了,赶快练习吧——【练习1】据行业统计,2010年上半年成品油表观消费量10963万吨,同比增长12.5%。
2010年上半年,全国成品油表观消费量同比增加了约多少万吨?
A.1009B.1218
C.1370D.1787
【铁哥精讲】
| 题型判断 | “增加了约多少万吨?” |
| 数据查找 | 现期量=10963万吨;r=12.5% |
| 直接套用 | r化为1/8,则套用结论:△x=10963÷(1+8)=10963÷9 |
| 参考答案 | 直除法计算出首两位为12。故此本题答案选B。 |
【练习2】2010年,我国黄金企业实现工业总产值2292.88亿元,同比增长66.72%;实现利润248.74亿元,同比增长78.19%。
2010年,我国黄金企业工业总产值同比增长了约多少亿元?( )A.918B.920
C.922D.924
【铁哥精讲】
| 题型判断 | “增加了约多少亿元?” |
| 数据查找 | 现期量=2292.88亿元;r=66.72% |
| 分子化1 | r约为2/3,此时无法直接使用结论,但只要r=1/n就可以直接套用,所以就需要把分子化为1,这个并不困难,2/3=1/1.5,则套用结论:△x=2292.88÷(1+1.5)=2292.88÷2.5 |
| 参考答案 | 直除三位为916。故此本题答案选A。 |
| 思路拓展 | 当r=m/n,我们只需将分子化为1即可快速套用结论。如:2/9=1/4.5、3/4≈1/1.3、8%=1/12.5…… |
【练习3】2010年1——6月,全国电信业务收入总量累计完成14860.7亿元,比上年同期增长21.4%;2010年1——6月我国电信业务收入总量比上年同期增长:( )A.2476.7亿元B.2619.6亿元
C.2972.0亿元D.3180.2亿元
【铁哥精讲】
| 题型判断 | “增加:( )亿元” |
| 数据查找 | 现期量=14860.7亿元;r=21.4% |
| 近似居中 | r=21.4%是介于1/5到1/4之间的,而不是某一个1/n或m/n。若强行将r化为1/5,势必需要分析误差,所以此处采用的办法是近似居中取中间,化r为1/4.5(即4和5取中间),则套用结论:△x=14860.7÷(1+4.5)=14860.7÷5.5 |
| 参考答案 | 直除两位为27。故此本题答案选B。 |
| 思路拓展 | 当r介于两个特殊分数之间的时候,我们可以采用近似居中取中间的办法。如:15.6%(介于1/6与1/7之间)化为1/6.5、18.5%(介于1/5与1/6之间)化为1/5.5…… |
【铁哥小结】
| 题型判断 | 增长(加)/增长(加)了多少…人、元、吨、个等 |
| 常用结论 |
若r=1/n,则: |
| 方法归纳 | ①若r=1/n,直接套用结论计算; |
| ②若r=m/n,将分子化为1后套用结论计算; | |
| ③若r介于两个特殊分数之间,采用近似居中取中间的办法。 |










